Hur extrem är extremsommaren?

Hett i 2018 års valrörelse

Juli 2018 var ovanligt varmt. Exakt hur varmt och hur ovanligt ska jag försöka reda ut här nedan. I samhällsdebatten har det diskuterats huruvida extremvärmen är ett exempel på det varmare klimatet, eller om det rör sig om naturliga variationer. Det har talats att värmen gynnar bl.a. Miljöpartiet och missgynnar bl.a. Sverigedemokraterna i 2018 års valrörelse. Mp säger att extremvärmen är en “Kraftig väckarklocka”. SD driver linjen att det till huvudsak rör sig om naturliga variationer och att man inte ska göra politik av vädret.

Vad kan man säga om vädret med statistik?

Jag vill ge ett statistiskt perspektiv på frågan. Jag ska med en enkel metod uppskatta hur extremt vädret är, och hur mycket som är naturlig variation.

Exakt formulera frågan

Jag tänker titta på medeltemperatur juli månad. Jag ska uppskatta

Hur extrem årets varma julimånad hade varit före industrialiseringen. Mer specifikt vad sannolikheten är att julimedeltemperaturen skulle vara lika hög eller högre än den från juli 2018.
Hur extrem extremvärmen är för dagens klimat. I analogi med punkt (1), hur sannolikt är det att julimedel blir lika hög eller högre idag.

Källor och antaganden

Jag tittar på endast stockholmsklimat. Dels för att vi har klimatdata som sträcker sig ända till 1756. Men framför allt för att det var enklast att hitta på nätet.

Det är en stor inskränkning och egentligen ganska ful statistik (mer om det senare). Men klimat är komplext och alla siffror jag kommer räkna blir inte särskilt tillförlitliga oavsett hur många väderstationer jag hämtar data från. Min modell kommer nämligen ha en del allvarliga brister.

Datat jag använder kommer från Stockholms temperaturserie på SMHI. Jag har också lagt datafilen lokalt på denna länk. Jag använder temperaturvärden ur kolumn 6 (som ska vara de mest kompletta och tillförlitliga). Jag plockar ut data fram till 1950. Det är ungefär då jag räknar med att värdens temperatur långsamt började stiga.

Normalfördelning

För att ta reda på om mätdata ser ut att komma ur en känd fördelning, kan man använda en Q-Q-plot. Man plottar teoretiska kvantiler till mätdatas kvantiler. Man kan också rita histogram. Jag hoppas att man kan anta att julimedel är normalfördelat.

Teorin säger att datat är av den sökta fördelningen om (de blå) punkterna ligger på (den röda) linjen. De ligger tillräckligt nära. För att kunna ge ett enkelt svar på frågan antar jag därmed att temperatur är normalfördelat.

Beräkningar

Hur extremt hade det varit att observera en minst lika varm sommar före 1950? Enligt SMHI är julimedeltemperaturen för 2018 22.4 grader. Medel och stickprovsstandardavvikelse för vår datamängd (1756-1950) är 16.765 och 1.678. Jag matar in det i fördelningsfunktionen för normalfördelning:

>>> import scipy.stats as sci_stats
>>> mu, sigma = 16.765, 1.678
>>> 1 - sci_stats.norm.cdf(22.4, mu, sigma)
0.00039230954826252606
>>> 1 / _
2549.0075488318707

Resultatet blev att det är ca 1 chans på 2500 att observera ett minst lika extremt värde. Med vår modell ska extremvärmen alltså ha inträffat i genomsnitt en gång på 2500 år före år 1950.

Hur extrem är extremvärmen med olika mycket temperaturhöjning?

Nu antar jag att julivädret fortfarande är normalfördelat, men att medel i normalfördelningen har förskjutits. Jag antar också att standardavvikelsen är densamma.

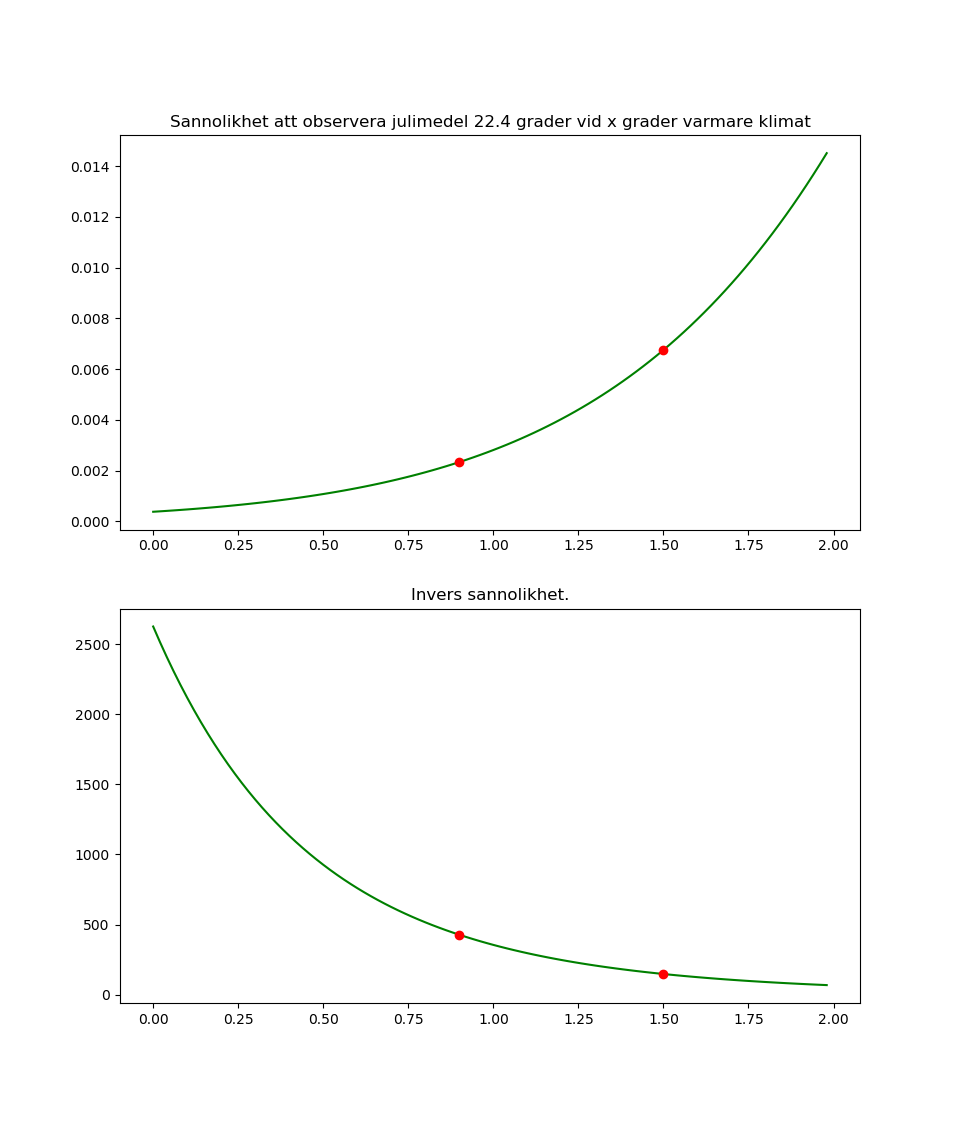
På SMHIs hemsida ser det ut som att Stockholmsvädret har blivit ca 1.5 grad varmare. Nasa säger att jordens medeltemperatur har blivit 0.9 grader varmare. Då är 1.5 grader rimligt för Stockholm. Huvudstaden värms ju upp av alla hus och bilar, inte bara av varmare klimat. Här är sannolikheterna i en graf. X-axeln är den antagna förskjutningen i medeltemperatur.

Slutsatser

Enligt vår modell brukade extremvärmen inträffa i genomsnitt en gång på 2500 somrar. Fram till 1950 då klimatförändringarna började märkas.
Med 0.9 grads varmare klimat inträffar en lika varm juli ungefär 1 gång på 400 år. Igen baserat på vår modell så klart.
Med 1.5 extra värme kan man räkna med extremjuli 1 gång på 140 somrar.

På ren svenska har den här typen av väder blivit 20 gånger vanligare. Men det är fortfarande ovanligt.

Jag vill också påpeka att få hade märkt skillnaden om medeltemperaturen i juli hade varit 21 grad istället för 22.4. Vi hade säkert haft en likadan klimatdebatt då också. Det är i den storleksordningen den globala uppvärmningen är.

Från ett statistiskt perspektiv kan jag därför inte säga att vare sig Jimmie Åkesson eller Isabella Lövin har fel.

Brasklappar

Hela den här artikeln är full med tveksam statistik. För det första:

Datat

Jag valde mätvärden från Stockholm och tittade speciellt på julimedelvärden. Hur vet du som läsare att jag inte testade flera mätstationer i Europa och flera sätt att mäta “värme”? Jag skulle kunna ha tagit medelvärde av dygnsminimumtemperaturer i Rom till exempel. Eller hundratals andra kombinationer av sätt att mäta värme eller torka och geografisk plats. Med vissa sätt att mäta skulle vi kommit fram till att hettan är så extrem att den aldrig skulle kunnat inträffa utan klimatförändring. Med andra hade den kanske hänt 1 gång på 100 år före 1950.

Republikaner vs demokrater

Ett exempel på min poäng är följande interaktiva demonstration. Här ska man välja ett sätt att mäta “ekonomi” och ett sätt att säga att “Republikanerna eller Demokraterna är vid makten”. Målet är att komma fram till att med stor sannolikhet är parti X bra (eller dåligt) för USAs ekonomi. Men det är så många sätt att mäta “bra för ekonomi” och “parti X vid makten” att man kan komma fram till alla 4 kombinationer av partier och bra eller dåligt.

Fördelningen

Jag antog att klimatdata är normalfördelat. Jag gjorde ett annat tekniskt antagande som jag inte poängterade: nämligen att data för olika år är helt oberoende. Båda dessa (speciellt det andra) kan ifrågasättas. Julimedelvärden kan till exempel vara sådana att ovanliga händelser är mycket mindre ovanliga än i en riktig normalfördelning. En matematisk fördelning med denna egenskap är Weibull-fördelningen.

Lögn, förbannad lögn och statistik

Jag har en riktlinje om statistik som jag försöker följa. Jag tror på statistisk slutsats (till exempel att Demokrater i USA skulle vara bra för landets ekonomi) om båda påståendena stämmer:

jag litar på att personen som gjort statistiken är objektiv och inte vill lura mig
personen som gjort statistiken kan statistik.

I det här fallet vet du antagligen ingenting om något av påståendena. Jag vill argumentera lite för båda:

Halva mitt budskap är att du inte ska tro på statistik. Och att vi egentligen inte kan säga något säkert om klimatet.
Jag (hävdar att jag) har läst strax under en och en halv termin ren och tillämpad statistik och sannolikhetsteori på högskolan. Jag sysslar då och då med lite enkel statistik i min yrkesverksamhet.

Hur kom det sig att jag skrev det här

Jag lyssnade på Expertpanelen på Kvartal. Lennart Bengtsson och Henning Rodhe diskuterade exakt den här frågan.

Källkod

Finner ni här